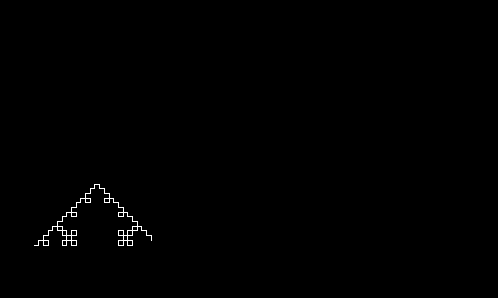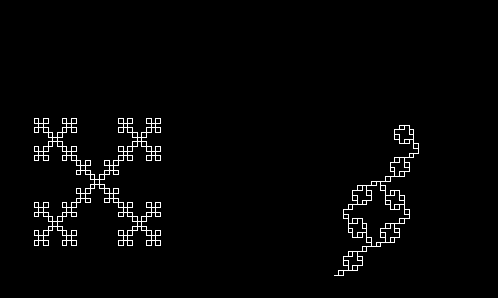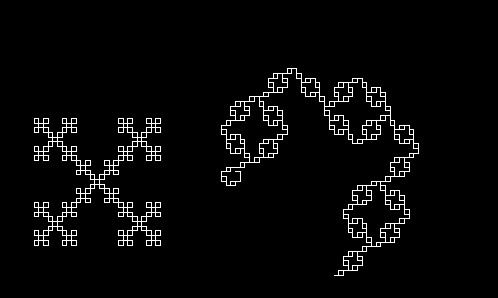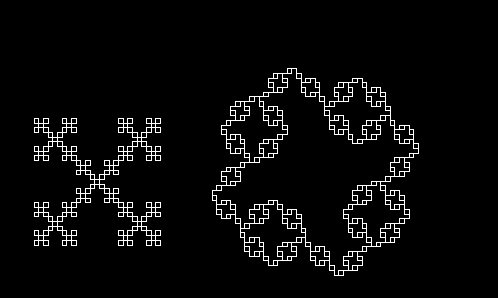
Understanding L Systems
Mar 19 2023
This week, I made a point to dive into something I've held an interest in for a long time, prodded on by the rediscovery of the book "The Algorithmic Beauty of Plants" whose mere title made such an impact that I have not been able to forget about it. It is a textbook all about the fascinating world of modeling plants algorithmically.
I could go on about all the things I want to do related to the topic of the textbook, but before I go on too long of a tangent, I'm going to stop myself short, and discuss (mostly for my own sake) the first framework needed to understand algorithmic plant modeling: L Systems.
L Systems?
Named after Aristid Lindenmayer, Lindenmayer Systems were first created with the intention of representing the development of cellular plant life and blah blah boring and certainly very important history.
The point is, I've known about them for a long time for the simple fact that "L Systems" is a term that comes up a lot alongside fractals, and just like most people that have even a marginal interest in math, programming, or just nature in general, I have found fractals as fascinating as they are elusive.
They main idea is pretty simple, but sounds complex at first. Before I say anything about it, just know that the L Systems create pretty shapes by repeating other shapes as much as you want, forever.
Got it? Okay, so you have a *grammar, *a generator and a producer.
Using the grammar, I can define a generator that spawns producers. Producers create more producers.
This is accomplished by giving a turtle simple but specific instructions.
Yes, a Turtle.
A helpful way to visualize L-Systems is by imagining a turtle that understands only the grammar defined by the L-System (this is not some cute metaphor I came up with, the turtle idea is in the textbook and has existed for a long time).
The turtle moves based on specific symbols, such as:
F: move forward +: turn clockwise -: turn counter-clockwise
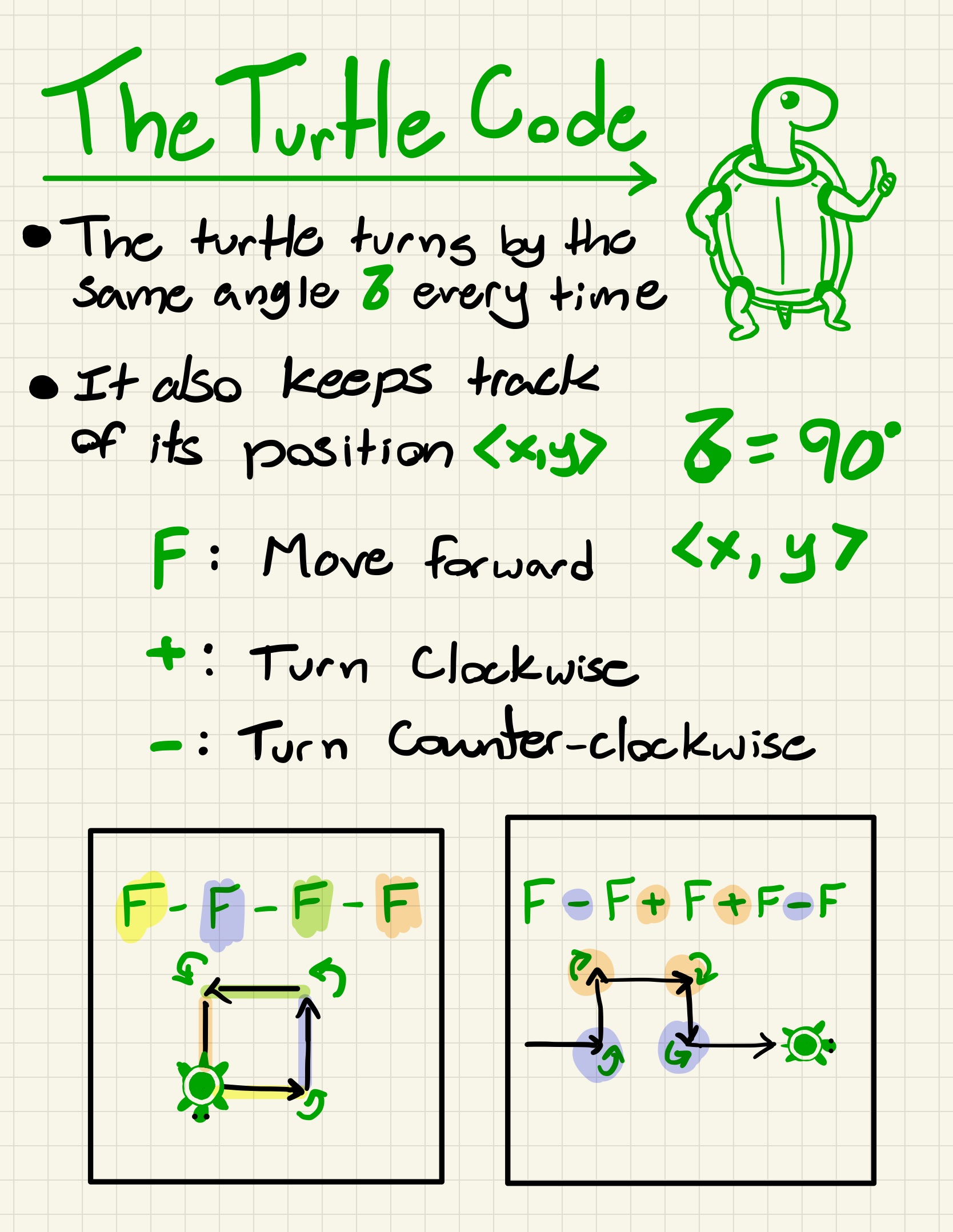
Generators and Producers
In an L-System, the generator serves as the initial shape or structure from which the pattern will be developed. The generator is a string composed of symbols, which are defined by the grammar. The producer, on the other hand, is responsible for interpreting the grammar and creating new shapes or structures based on the rules provided.
As the L-System iterates, the producer continually rewrites the generator string, replacing certain symbols with new ones according to the grammar rules. The process of rewriting allows the pattern to grow and evolve, generating intricate and complex patterns over time.
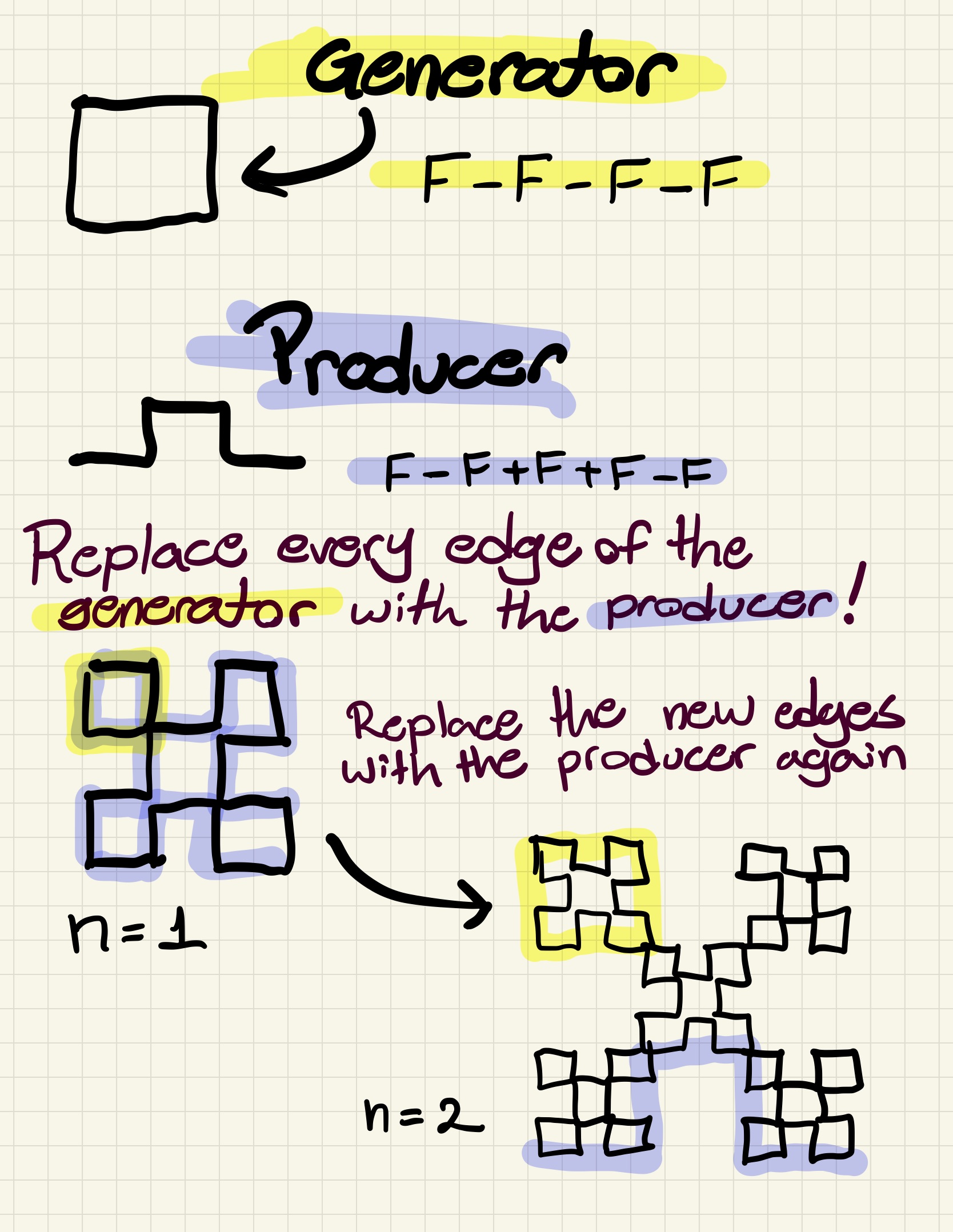
Starting to Code
To gain a better understanding of L-Systems, I created a simple program in C using the SDL2 library. The program sets up an SDL environment and displays a window with the resulting L-System pattern.
First, I defined the initial turtle state and created a function called interpret_sequence to take in a string representing a sequence of rules, such as "F+F-F-F+F-." The turtle would then move according to these rules.
Then, right after setting the draw color I insert the first touch of L system magic
const char *generator = "F-F-F-F-F";
// Define the L-system parameters
const float angle = 90.0f; // angle in degrees
const float scale = 10.0f; // length of each line segment
typedef struct
{
float x;
float y;
float angle;
} TurtleState;
// Define a function to interpret the L-system sequence
void interpret_sequence(SDL_Renderer *renderer, const char *sequence, TurtleState *state)
{
while (*sequence)
{
switch (*sequence)
{
case 'F': // move forward
float x1 = state->x;
float y1 = state->y;
state->x += scale * cos(state->angle * M_PI / 180.0f);
state->y += scale * sin(state->angle * M_PI / 180.0f);
float x2 = state->x;
float y2 = state->y;
SDL_RenderDrawLine(renderer, x1, y1, x2, y2);
break;
case '+': // turn left
state->angle += angle;
break;
case '-': // turn right
state->angle -= angle;
break;
}
++sequence;
}
}
After compiling and running the program, I was able to create a simple L-System pattern.
gcc garden.c -o garden -lSDL2 -lm
./garden
A square! Breathtaking, I know.
What I just wrote was a zero iteration parser, meaning there's no depth, recursion, or rewriting of anything. The shape is unsurprisingly simple. In L-System terms, that square is defined by the string F-F-F-F, and it was written by a "turtle" that makes 90 degree turns.
Now what happens when we replace the square's edges with a new shape?
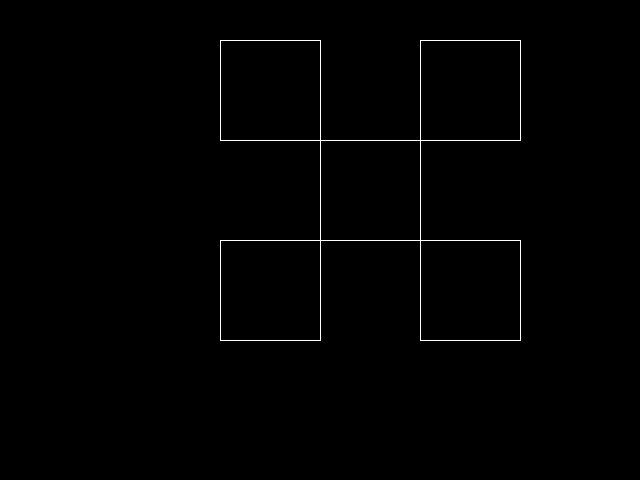
This is what happens when you replace each F of the generator with a new string (called the producer) F-F+F+F-F
Now this is pod racing.
We can keep doing this infinitely, replacing the edge again and again with the same shape. Let's say I do this n times. The shape above is the result when n=1. So let's see what we get when I keep going.
n=2
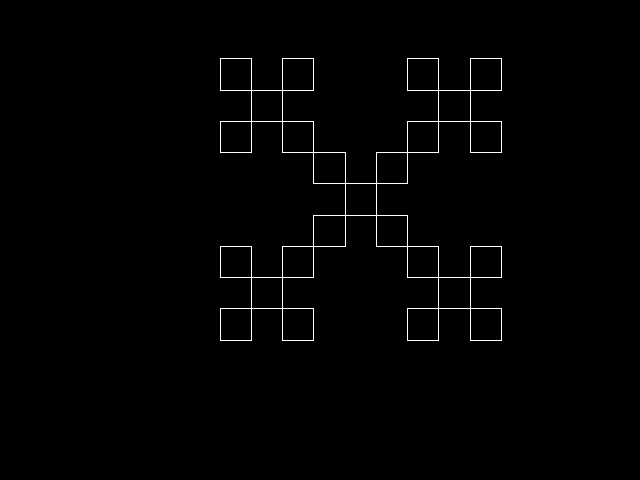
n=3

These images demonstrate the iterative nature of L-Systems, where each iteration adds complexity to the pattern. Through the simple process of rewriting and following the specified grammar, L-Systems can generate intricate and mesmerizing patterns reminiscent of natural structures. I am excited to keep diving into the topic, and eventually learn the intricacies of modeling plant life.
The code I wrote for this post can be found here: https://github.com/kaiobarb/LSystems
Thanks for reading!